今日からはじめるレコメンデーション -探索と利用のジレンマとベイジアンアプローチ-

前回の記事では平均評価による推薦の問題点とその解決策について紹介しました。推薦の際に確信度が考慮されない問題点を信頼区間で、評価数が0の場合にスコアが不定になる問題点をスムージングによって解決する方法について紹介しました。

hironsan.hatenablog.com

今回は情報推薦における探索と利用のジレンマとその解決策としてのベイジアンアプローチについて紹介します。

探索と利用のジレンマ

探索（Exploration）と利用（Exploitation）のジレンマとは、有用そうな選択肢を選んでいると、他の選択肢がより有用であることを発見する機会が失われ、他の選択肢ばかりを試していると、有用そうな選択肢を利用できないというジレンマです。

ぼくはチーズバーガーが大好きです。しかし、チーズバーガーばかり食べていると他のより美味いハンバーガーを発見する機会がなくなります。かといって、アボガドバーガーや照り焼きバーガーなどのバーガーばかり食べているとチーズバーガを食べることができません。

もう少し真面目な例として、スロットマシンのプレイを挙げられます。スロットマシンでなるべく多くのコインを得るためには、どのマシンが良いか調べる必要があります。そのためには、実際にプレイしてスコアを出す方法が考えられます。仮に、勝利を1、負けを0とするとスコアは $P(win) = \frac{＃win}{＃total}$ で計算できます。たとえば、3回プレイして1回勝つとスコアは $P(win) = \frac{1}{3}$ です。

ここで問題となるのは、いったい何回プレイすればいいのかという点です。信頼区間的には、3回プレイして1回勝つより、300回プレイして100回勝つ方が信頼区間は狭くなって良い推定と言えます。つまり、プレイ数が少なすぎればあまり良い推定はできません。一方、プレイ数が多ければ良い推定はできますがその分コストがかかります。

このように、良い推定をするためにはより多くのデータを集める必要があるのですが、より多くのデータを集めるには局所最適な部分にもコストをかけなければならないというジレンマがあります。データを集めるほどよい推定ができるが、最高の解を利用したくもある。しかし、集めるときは利用できないし、利用するためには集めることができない。

探索と利用のジレンマは情報推薦にも関係しています。たとえば、YouTubeで猫の動画を見まくった場合、レコメンデーションシステムはそれを学んで、猫の動画を推薦してくるかもしれません。しかし、普通に考えると、他の動画も見たいはずです。これは利用はしているけど探索はしていない状態で、局所最適に陥っています。一方で、たとえ探索して推薦しても良いことは保証されません。このように、推薦においても探索と利用のジレンマは見られます。

ここまでで探索と利用をなるべくバランスよく行いたいということはなんとなく理解できました。次に問題となるのは、実際にどうやるかです。その方法の一つが、次に紹介するベイジアンアプローチです。

ベイジアンアプローチ

ベイジアンによるアプローチでは確率分布のパラメータも確率変数と考えます。たとえば、ベルヌーイ分布は $f(k;\pi) = \pi^{k}(1-\pi)^{1-k}$ という形の分布で、パラメータとして $\pi$ を持ちますが、この $\pi$ も確率変数として考えます。確率変数が従う分布としてはベータ分布が使われます。

ベイズでない場合は尤度関数を定義して、最適なパラメータである $\hat{\pi}$ を最尤推定していました。ベイズの場合は $\pi$ は確率分布なので、もはや $\hat{\pi}$ は固定値ではなくそれ自身が確率分布を持っています。したがって、形としては $p(\pi|x_1,\ldots, x_N) = p(\pi|X)$ のように表すことができます。なので、たとえばコインを100回投げて、その結果を使って $\pi$ の分布を推定します。

ここで重要となるのが以下のベイズの定理です。

$\displaystyle{ p(\pi|X) = \frac{p(X|\pi)p(\pi)}{\int p(X|\pi)p(\pi)} }$

言葉で書くと以下のようになるでしょう。

$\displaystyle{ \piの事後確率 = \frac{尤度 \cdot 事前確率}{正規化項} }$

$p(\pi|X)$ は事後確率で、要するにデータ $X$ を観測した後のパラメータ $\pi$ の分布です。 $p(X|\pi)$ はパラメータ $\pi$ の元でのデータXの出現確率を表しています。 $p(\pi)$ は事前確率で、ここにベータ分布を使っていきます。少々複雑な式に見えますが、実際には分母を計算する必要がないので、 $p(\pi|X) \propto p(X|\pi)p(\pi)$ のようにシンプルになります。

実際に $p(\pi|X)$ をシミュレーションしてみましょう。以下はmachine_learning_examplesのbayesian_bandit.pyを使ってシミュレーションした結果です。データを集めるほど $p(\pi|X)$ の形が細くなり、確信度が上がっていくということを表現できています。

f:id:Hironsan:20190426092821p:plain — 事後分布のシミュレーション結果

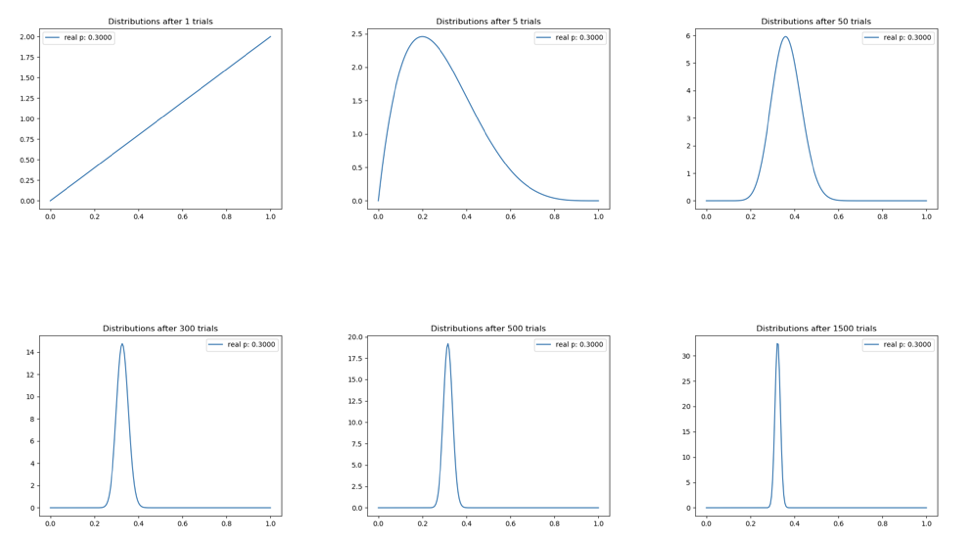
事後分布を使うときは、分布から値をサンプリングして使います。ベイズでない場合は値が一つに決まるのでそれを使えばいいのですが、ベイズの場合は分布なので、そこからサンプリングして使うというわけです。

ベイズを使うことで使うことで、探索と利用を上手くバランスさせることができます。たとえば、以下の2つの分布について考えてみましょう。

f:id:Hironsan:20190426154823p:plain

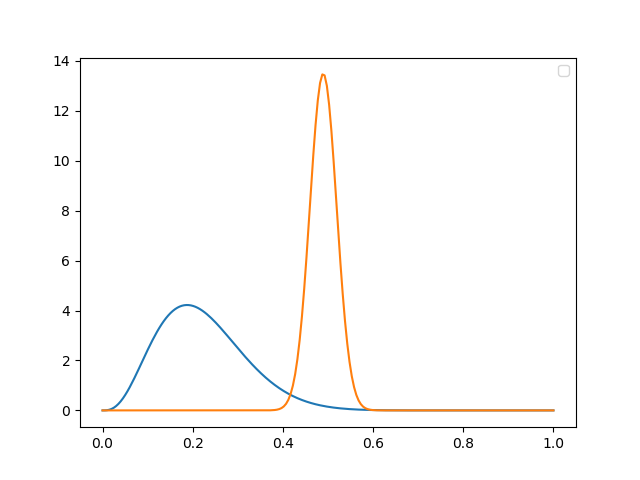
2つの分布は狭い形と広い形をしています。狭い形の方はデータを多く集められていて、広い方は少ないと考えられます。ここからサンプリングすると、p(0.42<x<0.58)の範囲では狭い分布からサンプリングされる可能性が高く、それより小さい範囲では広い分布からサンプリングされる可能性が高くなっています。それにより、両方の分布を探索でき、かつ、狭い分布の知識を利用できるので探索と利用をバランスさせることができます。