確率的ブロックモデルによる関係データのクラスタリング

本記事では、確率的ブロックモデル（Stochastic Block Model; SBM）の概要と周辺化ギブスサンプラーによる推論について簡単に解説した後、Pythonを用いた実装例を示します。さらに、Zachary’s Karate Clubデータセットを用いて、確率的ブロックモデルをクラスタリングに適用し、その結果をARI（Adjusted Rand Index）で評価します。

確率的ブロックモデルとは？

確率的ブロックモデルは、関係データのクラスタリングに用いられる確率的生成モデルです。確率的ブロックモデルでは、関係データに潜在的なブロック構造が存在すると仮定し、その推論を通じてクラスタリングを行います。具体的には、オブジェクト（関係データ行列のインデックス）間の関係の有無は、各オブジェクトが属するクラスター間の関係の強さで近似できると仮定しています。

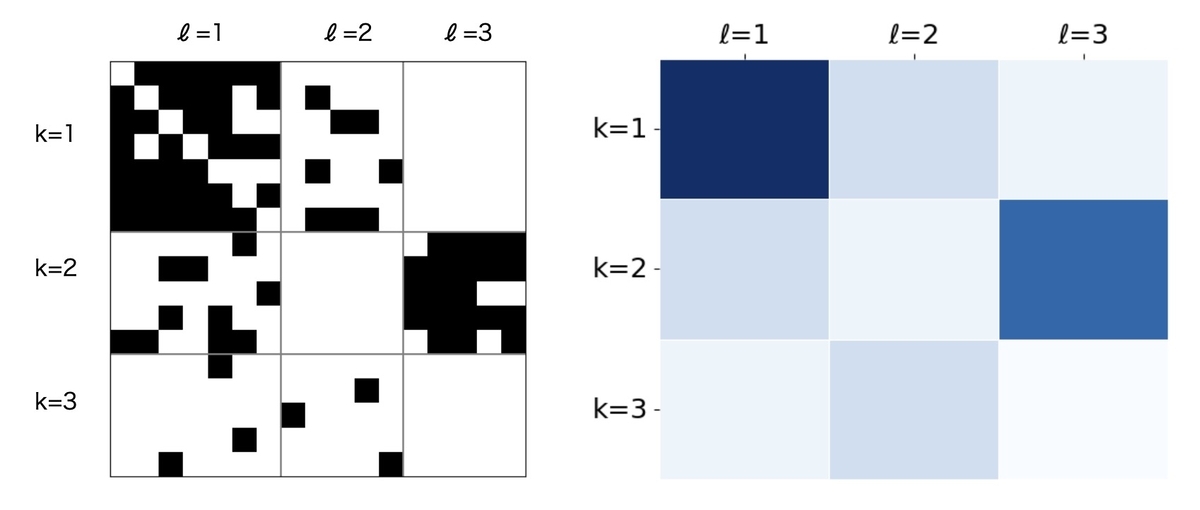
確率的ブロックモデルのブロック構造。左側は関係データ行列で、行と列にそれぞれK=3とL=3個のクラスターがあると仮定している。なお、クラスター数が同じである必要はない。右側は左側の図を抽象化したもので、色の濃さはクラスター同士の関係の強さを表している

確率的ブロックモデルは、以下のように定式化されます。関係データ行列 $\boldsymbol{X} = (x_{i,j}) \in \{0, 1\}^{N_1 \times N_2}$ が与えられたとき、行と列に対するクラスターの割り当てを表す変数 $Z_1 = (z_{1,i}) \in \{1,\ldots,K\}^{N_1}$ と $Z_2 = (z_{2,j}) \in \{1,\ldots,L\}^{N_2}$ を導入します。KとLはそれぞれ行と列のクラスター数に対応しています。このとき、関係データ行列 $\boldsymbol{X}$ の要素 $x_{i,j}$ は、行のクラスター $z_{1,i}$ と列のクラスター $z_{2,j}$ の関係の強さ $\theta_{z_{1,i}, z_{2,j}}$ に依存して次のように生成されると仮定します。

$\displaystyle \begin{align} \boldsymbol{\pi}_1 &\sim \text{Dirichlet}(\boldsymbol{\alpha}_1) \\ \boldsymbol{\pi}_2 &\sim \text{Dirichlet}(\boldsymbol{\alpha}_2) \\ z_{1,i} &\sim \text{Categorical}(\boldsymbol{\pi}_1) \\ z_{2,j} &\sim \text{Categorical}(\boldsymbol{\pi}_2) \\ \theta_{k,l} &\sim \text{Beta}(a_{k,l}, b_{k,l}) \\ x_{i,j} &\sim \text{Bernoulli}(\theta_{z_{1,i}, z_{2,j}}) \end{align}$

確率的ブロックモデルの推論

推論では、周辺化ギブスサンプラーを用いて、行と列に対するクラスターの割り当て（ $z_{1,i}$ と $z_{2,j}$ ）を推定します。周辺化ギブスサンプラーは、MCMC法の一種で、モデルのパラメーターを周辺化して、目的変数の事後分布をサンプリングする手法です。具体的には、クラスターの割り当てをランダムに初期化し、各オブジェクトのクラスターを順番にサンプリングします。このとき、他のオブジェクトのクラスター割り当ては固定されていると仮定します。

確率的ブロックモデルにおける推論式の導出については、『関係データ学習』を参照してもらうとして、 $z_{1,i}$ をサンプリングするための事後分布は以下の式で定義されます。ここで、 $N_1$ と $N_2$ は関係データ行列 $\boldsymbol{X}$ の行数と列数、Lは列側のクラスター数、 $\boldsymbol{Z}_1^{\backslash(i)}$ は行のクラスター割り当てのうち $i$ 行目を除いたもの、 $\boldsymbol{Z}_2$ は列のクラスター割り当てを表します。

$\displaystyle \begin{split} p(z_{1,i}=k|\boldsymbol{X}, \boldsymbol{Z}_1^{\backslash(i)}, \boldsymbol{Z}_2) &\propto \hat{\alpha}_{1,k} \prod_{l=1}^{L} \frac{\Gamma(\hat{a}_{k,l} + \hat{b}_{k,l})}{\Gamma(\hat{a}_{k,l}) \Gamma(\hat{b}_{k,l})} \\ &\quad \times \frac{\Gamma \left( \hat{a}_{k,l} + \sum_{j=1}^{N_2} x_{i,j} \mathbb{I}(z_{2,j} = l) \right) \Gamma \left( \hat{b}_{k,l} + \sum_{j=1}^{N_2} (1 - x_{i,j}) \mathbb{I}(z_{2,j} = l) \right)}{\Gamma \left( \hat{a}_{k,l} + \hat{b}_{k,l} + \sum_{j=1}^{N_2} \mathbb{I}(z_{2,j} = l) \right)} \end{split}$

その他の更新に必要な統計量の定義を以下に示します。 $m_{1,k}$ はクラスターkに属するオブジェクト数、 $n_{k,l}^{(+)}$ と $n_{k,l}^{(-)}$ は行方向のk番目のクラスターと列方向のl番目のクラスターで定義される関係データ行列のブロック(k, l)におけるx=1とx=0になる要素数を示しています。

$\displaystyle \begin{align} m_{1,k} &= \sum_{i=1}^{N_1} \mathbb{I}(z_{1,i} = k) \\ n_{k,l}^{(+)} &= \sum_{i=1}^{N_1} \sum_{j=1}^{N_2} x_{i,j} \mathbb{I}(z_{1,i} = k) \mathbb{I}(z_{2,j} = l) \\ n_{k,l}^{(-)} &= \sum_{i=1}^{N_1} \sum_{j=1}^{N_2} (1 - x_{i,j}) \mathbb{I}(z_{1,i} = k) \mathbb{I}(z_{2,j} = l) \end{align}$

$z_{1,i}$ をサンプリングする際は、 $z_{1,i}$ はクラスターの割り当てを解除して扱うため、以下のように $z_{1,i}$ の割り当てを除いた $\hat{m}_{1,k}$ 、 $\hat{n}_{k,l}^{(+)}$ 、 $\hat{n}_{k,l}^{(-)}$ を定義します。

$\displaystyle \begin{align} \hat{m}_{1,k} &= \sum_{\substack{i' \neq i, \\ i' = 1}}^{N_1} \mathbb{I}(z_{1,i'} = k) = m_{1,k} - \mathbb{I}(z_{1,i} = k) \\ \hat{n}_{k,l}^{(+)} &= \sum_{\substack{i' \neq i, \\ i' = 1}}^{N_1} \sum_{j=1}^{N_2} x_{i',j} \mathbb{I}(z_{1,i'} = k) \mathbb{I}(z_{2,j} = l) \\ &= n_{k,l}^{(+)} - \mathbb{I}(z_{1,i} = k) \sum_{j=1}^{N_2} x_{i,j} \mathbb{I}(z_{2,j} = l) \\ \hat{n}_{k,l}^{(-)} &= \sum_{\substack{i' \neq i, \\ i' = 1}}^{N_1} \sum_{j=1}^{N_2} (1 - x_{i',j}) \mathbb{I}(z_{1,i'} = k) \mathbb{I}(z_{2,j} = l) \\ &= n_{k,l}^{(-)} - \mathbb{I}(z_{1,i} = k) \sum_{j=1}^{N_2} (1 - x_{i,j}) \mathbb{I}(z_{2,j} = l) \end{align}$

上記で定義した $\hat{m}_{1,k}$ 、 $\hat{n}_{k,l}^{(+)}$ 、 $\hat{n}_{k,l}^{(-)}$ を用いて、 $\hat{\alpha}_{1,k}$ 、 $\hat{a}_{k,l}$ 、 $\hat{b}_{k,l}$ を以下のように定義します。ここで、 $\alpha_{1,k}$ はDirichlet分布のハイパーパラメーター、 $a_0$ と $b_0$ はBeta分布のハイパーパラメーターです。

$\displaystyle \begin{align} \hat{\alpha}_{1,k} &= \alpha_{1,k} + \hat{m}_{1,k} \\ \hat{a}_{k,l} &= a_0 + \hat{n}_{k,l}^{(+)} \\ \hat{b}_{k,l} &= b_0 + \hat{n}_{k,l}^{(-)} \end{align}$

サンプリングの結果、新しいクラスターの割り当て $z_{1,i}$ が決定したら、以下に示すように統計量を更新して次のオブジェクトの処理に進みます。 $z_{2,j}$ についても同様の手続きで更新します。このように、すべてのオブジェクトに対してクラスターの割り当てを更新することを繰り返すことで、周辺化ギブスサンプラーによる推論が完了します。

$\displaystyle \begin{align} m_{1,k} &= \hat{m}_{1,k} + \mathbb{I}(z_{1,i} = k) \\ n_{k,l}^{(+)} &= \hat{n}_{k,l}^{(+)} + \mathbb{I}(z_{1,i} = k) \sum_{j=1}^{N_2} x_{i,j} \mathbb{I}(z_{2,j} = l) \\ n_{k,l}^{(-)} &= \hat{n}_{k,l}^{(-)} + \mathbb{I}(z_{1,i} = k) \sum_{j=1}^{N_2} (1 - x_{i,j}) \mathbb{I}(z_{2,j} = l) \end{align}$

確率的ブロックモデルの推論の実装

ここでは、Zachary’s Karate Clubデータセットを使い、周辺化ギブスサンプラーにより確率的ブロックモデルを推論する実装例を示します。あくまで学習・検証を目的としたサンプルコードです。

まずは必要なパッケージをインストールします。

pip install numpy networkx matplotlib scipy scikit-learn tqdm

パッケージをインストールしたら、インポートします。

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import numpy.typing as npt
import tqdm
from scipy.special import betaln, logsumexp
from sklearn.metrics import adjusted_rand_score

次に、Zachary’s Karate Clubデータセットを読み込みます。このデータセットは34の頂点からなる無向グラフで、各頂点は空手クラブのメンバーを表しています。エッジの有無はメンバー間の交友の有無を表しています。この空手クラブは、最終的に2つのグループに分裂してしまいます。そのため、クラスタリングによりこの分裂を予測できるか確認するために使うことができます。

def load_dataset() -> tuple[npt.NDArray, npt.NDArray]:
    # 空手クラブのグラフを読み込む
    graph = nx.karate_club_graph()

    # グラフを行列に変換
    X = (nx.to_numpy_array(graph) > 0).astype(np.int32)
    np.fill_diagonal(X, 1)

    # クラブ情報を数値に変換
    mapping = {"Mr. Hi": 0, "Officer": 1}
    Z = [mapping[node["club"]] for node in graph.nodes.values()]

    return X, np.array(Z)

X, Z = load_dataset()

データセットを読み込んだら、可視化してみます。

# 関係データを可視化。X=1は黒、X=0は白
plt.imshow(X, cmap="gray_r")
plt.show()

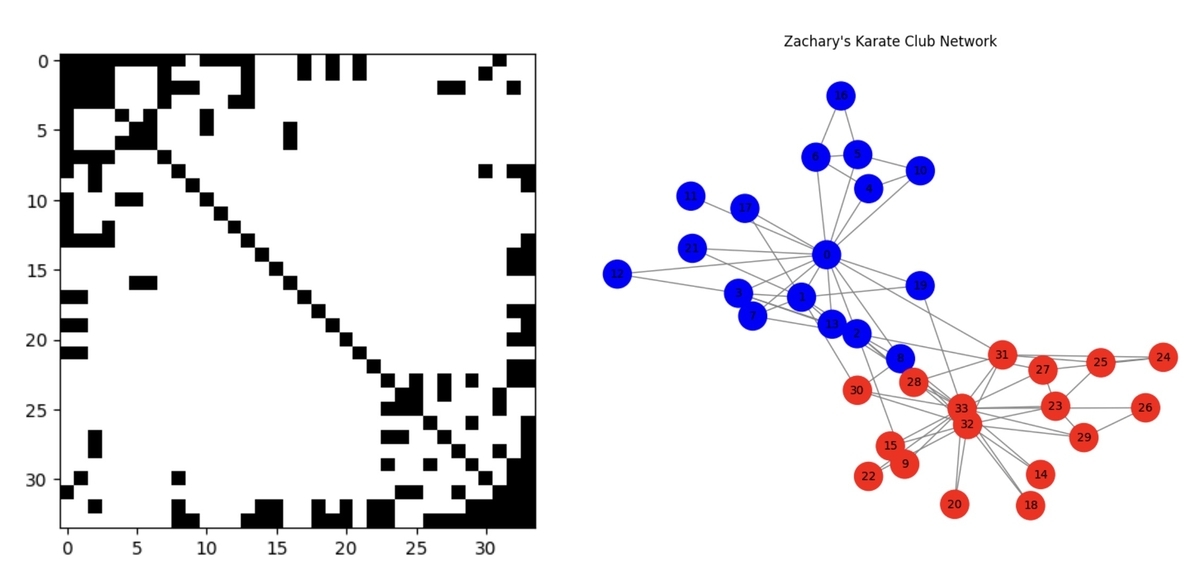
関係データ行列を可視化すると、以下のようになります（下図左）。黒は交友があること、白は交友がないことを表しています。参考までにグラフ表現として可視化した例も示しておきます（下図右）。

次に、周辺化ギブスサンプラーによる確率的ブロックモデルの推論をするための関数を定義します。この関数は、行列 X とクラスター数 K および L、Dirichlet分布のハイパーパラメーター alpha1 と alpha2、Beta分布のハイパーパラメーター a0 と b0、反復回数 num_iter を引数に取ります。関数内では、周辺化ギブスサンプラーによりクラスターの割り当てをします。

def collapsed_gibbs_sampler(
    X: npt.NDArray,
    K: int,
    L: int,
    alpha1: npt.NDArray,
    alpha2: npt.NDArray,
    a0: float,
    b0: float,
    num_iter: int,
) -> tuple[npt.NDArray, npt.NDArray]:
    """周辺化済みギブスサンプラーによるSBMのクラスター割り当て.

    Args:
        X (npt.NDArray) : [N1 x N2] の隣接行列(0/1)
        K (int) : 行側のクラスター数
        L (int) : 列側のクラスター数
        alpha1 (npt.NDArray) : 行側のDirichlet分布のハイパーパラメーター
        alpha2 (npt.NDArray) : 列側のDirichlet分布のハイパーパラメーター
        a0 (float) : Beta分布のハイパーパラメーター
        b0 (float) : Beta分布のハイパーパラメーター
        num_iter (int): ギブスサンプラーの反復回数

    Returns:
        z1 (npt.NDArray) : 最終的なクラスター割り当て(行)
        z2 (npt.NDArray): 最終的なクラスター割り当て(列)
    """
    N1, N2 = X.shape
    rng = np.random.default_rng()

    # ランダムに初期化
    z1 = rng.choice(K, size=N1)
    z2 = rng.choice(L, size=N2)

    z1_onehot = np.eye(K)[z1]
    z2_onehot = np.eye(L)[z2]

    # 各統計量の計算
    m1 = np.bincount(z1, minlength=K)
    m2 = np.bincount(z2, minlength=L)
    n_pos = z1_onehot.T @ X @ z2_onehot
    n_neg = z1_onehot.T @ (1 - X) @ z2_onehot

    # ギブスサンプラーの反復
    for _ in tqdm.tqdm(range(num_iter)):
        # 行の更新
        for i in range(N1):
            # 現在の行iの寄与を各ブロックから除去
            k = z1[i]
            m1[k] -= 1
            for j in range(N2):
                l = z2[j]
                n_pos[k, l] -= X[i, j]
                n_neg[k, l] -= 1 - X[i, j]

            # 候補となる各クラスターkに対する対数確率を計算
            log_probs = np.zeros(K)
            for k in range(K):
                log_probs[k] = np.log(alpha1[k] + m1[k])
                for l in range(L):
                    a_hat_kl = a0 + n_pos[k, l]
                    b_hat_kl = b0 + n_neg[k, l]
                    log_probs[k] += betaln(
                        a_hat_kl + np.sum(X[i][z2 == l]),
                        b_hat_kl + np.sum((1 - X[i])[z2 == l]),
                    ) - betaln(a_hat_kl, b_hat_kl)
            # 正規化してサンプリング
            probs = np.exp(log_probs - logsumexp(log_probs))
            k = rng.choice(K, p=probs)
            z1[i] = k
            # 統計量の更新
            m1[k] += 1
            for j in range(N2):
                l = z2[j]
                n_pos[k, l] += X[i, j]
                n_neg[k, l] += 1 - X[i, j]

        # 列の更新
        for j in range(N2):
            l = z2[j]
            m2[l] -= 1
            for i in range(N1):
                k = z1[i]
                n_pos[k, l] -= X[i, j]
                n_neg[k, l] -= 1 - X[i, j]

            log_probs = np.zeros(L)
            for l in range(L):
                log_probs[l] = np.log(alpha2[l] + m2[l])
                for k in range(K):
                    a_hat_kl = a0 + n_pos[k, l]
                    b_hat_kl = b0 + n_neg[k, l]
                    log_probs[l] += betaln(
                        a_hat_kl + np.sum(X[z1 == k, j]),
                        b_hat_kl + np.sum((1 - X[:, j])[z1 == k]),
                    ) - betaln(a_hat_kl, b_hat_kl)

            probs = np.exp(log_probs - logsumexp(log_probs))
            l = rng.choice(L, p=probs)
            z2[j] = l
            m2[l] += 1
            for i in range(N1):
                k = z1[i]
                n_pos[k, l] += X[i, j]
                n_neg[k, l] += 1 - X[i, j]

    return z1, z2

推論のための関数を定義したので、読み込んだデータセットを用いて推論をします。パラメーターの設定については、『関係データ学習』の79ページに記載されていたIRMでの推奨設定を参考に決定しています。また、クラスター数についても81ページに記載されていたIRMでの結果と比較したいため、それぞれ4と設定しています。

# パラメータ設定
K, L = 4, 4         # クラスター数（行側と列側）
alpha1 = np.ones(K) # Dirichlet分布のハイパーパラメーター（行側）
alpha2 = np.ones(L) # Dirichlet分布のハイパーパラメーター（列側）
a0, b0 = 1.0, 1.0   # Beta分布のハイパーパラメーター
num_iter = 10000

# 周辺化ギブスサンプラーの実行
z1, z2 = collapsed_gibbs_sampler(
    X, K, L, alpha1, alpha2, a0, b0, num_iter=num_iter
)

推論を終えたら、ARI（Adjusted Rand Index）を用いてクラスタリングの性能を評価します。それぞれ、行と列のクラスタリング結果に対応しています。

print(adjusted_rand_score(Z, z1))
print(adjusted_rand_score(Z, z2))

0.6404445412943996
0.7274505542273418

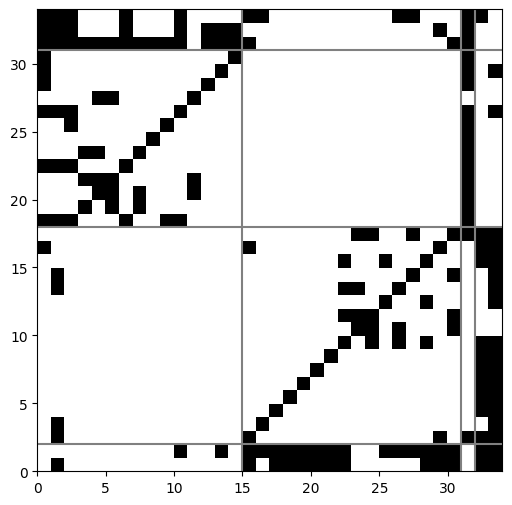
クラスタリングの性能は、ARIで0.6404と0.7275となりました。関係データ学習の本に記載されていたIRMでの例では、行と列のクラスタリング結果に対するARIはそれぞれ0.6077と0.6404だったので、それに近い性能が得られていることを確認できました。この結果から、今回実装した推論用のコードを使うことで、一定の性能でクラスター構造を推論できることがわかります。

最後に、得られたクラスターを可視化した結果を載せます。

まとめ

本記事では、確率的ブロックモデル（SBM）の概要と周辺化ギブスサンプラーによる推論を説明し、Pythonによる実装例を示しました。今回は対称関係データに対してクラスタリングを行いましたが、確率的ブロックモデルは非対称関係データにも適用可能です。実装を通じて理解が深まったため、機会があれば利用してみたいと思います。

Ahogrammer

Deep Dive Into NLP, ML and Cloud

確率的ブロックモデルによる関係データのクラスタリング

確率的ブロックモデルとは？

確率的ブロックモデルの推論

確率的ブロックモデルの推論の実装

まとめ

参考文献