前回の記事では人気度と新規性、またそれらをハイブリッドした手法による推薦の方法について紹介しました。そこでは、人気度と新規性に基づく手法の問題点とその解決方法について説明しました。
今回は、平均評価に基づく推薦の問題点とその解決策について紹介します。今回紹介する問題点は以下の2つです。
- 確信度が考慮されていない
- 評価数が0の場合にスコアが不定になる
平均評価による推薦について考えるため、みなさんがECサイトを運営しているとしましょう。みなさんは運営しているECサイトで、平均評価によるレコメンデーションの実装を検討しています。平均評価による推薦では、商品の平均的な評価の大小に基づいて商品を推薦します。たとえば、Amazonでイヤホンを検索して評価順に並べると以下のような結果になります。

平均評価による推薦は悪くなさそうですが、確信度(confidence)が考慮されていないという問題があります。たとえば、 一つの評価しかないけど星5の商品と、50000の評価があるけど星4.2の商品がある場合、平均評価による推薦では前者が推薦されます。これでは評価の高い新商品ばかり推薦されてしまうことでしょう。
信頼区間の導入
確信度を考慮する方法の一つとして信頼区間(Confidence Interval, CI)を使った方法があります。信頼区間は統計学でお馴染みの概念ですが、確信度を考慮するために使うこともできます。情報推薦においては信頼区間の下限を使って候補のランク付けを行うことができます。以下に信頼区間の図を示しました。
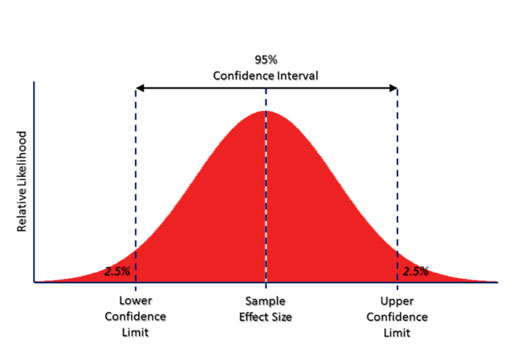
信頼区間を使った推薦について、もう少し具体的に説明します。
たとえば、2つの商品A, Bがあり、どちらも平均で星4の評価だったとします。ここで、商品Aの評価数は3、商品Bの評価数は100とします。このとき、2つの商品に対する信頼区間のグラフを描くと、商品Bのグラフが尖った形になり、下限の値も大きくなります。したがって、同じ平均評価でもその下限を使うことで、商品Bを推薦することができます。以下に示したように、イメージとしては、評価数が増えるほどグラフが尖った形になります。
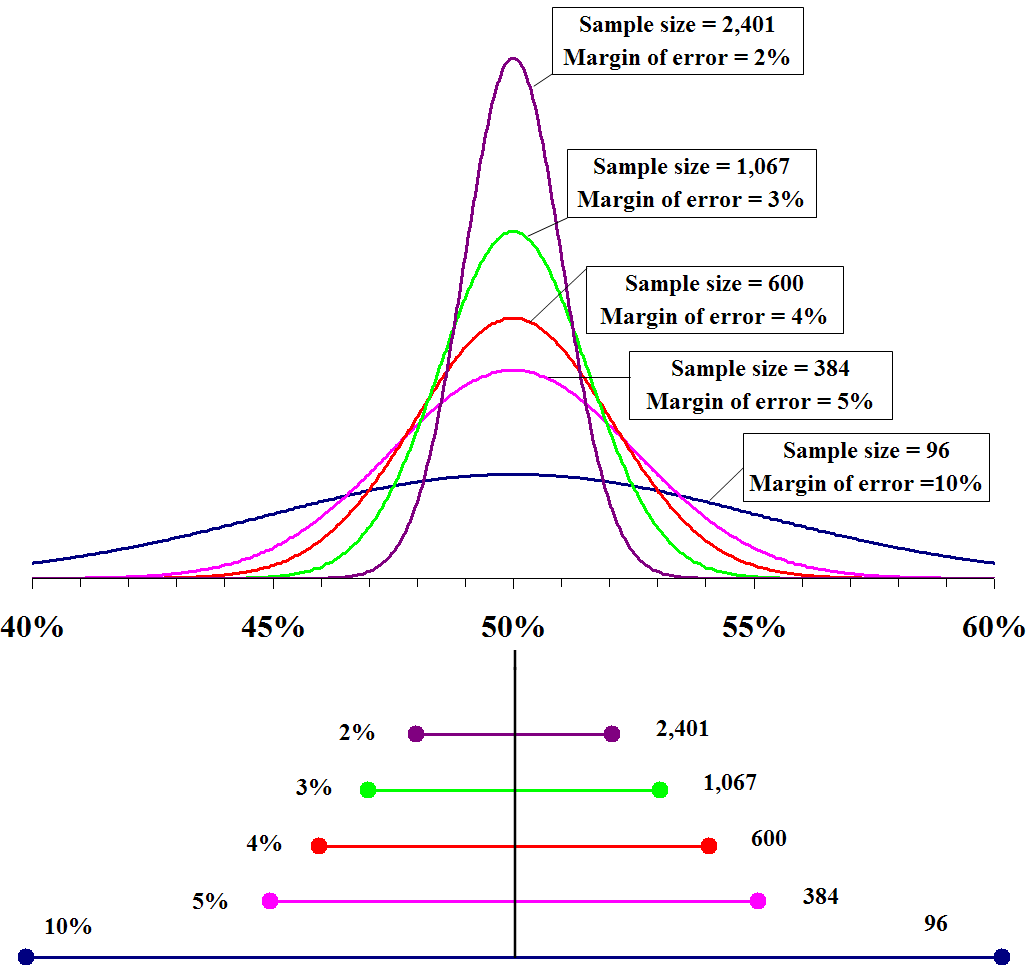
ここまでは概念的な説明をしてきましたが、評価数が多くなるとグラフの形が尖る話をもう少し数学的に説明します。
数学的な説明をするために、N個の評価が平均
、分散
の正規分布
に従って独立に付けられると仮定します。そうすると、正規分布の再生性によりその和の分布
も正規分布
に従います。和の分布から平均値の分布を求めるとその分散は
となります。したがって、評価数が多くなるほど、分散が小さくなり、正規分布の形が細長くなるというわけです。この辺の話は、正規分布の再生性と分散の定数倍の公式を使えば証明できます。詳細についてはAppendixに示したので参照してください。
このようにして、平均評価の分布が正規分布に従うことがわかれば、その信頼区間の下限を求めることは比較的容易にできます。たとえば、95%信頼区間を使うのだとすれば、その下限は「平均 - 1.96×標準偏差」で求めることができます。この1.96という値は正規分布表を参照することでわかります。
ここまでは各評価が正規分布に従っていることを仮定していましたが、正規分布に従っていない場合はどうなるのでしょうか?その場合も問題なく扱うことができます。なぜなら、評価がどんな分布に従っているのであれ、中心極限定理によりその平均の分布は正規分布に従うからです。式で示すと、以下のがどんな分布に従っているのであれ、
は正規分布に従います。
正規分布以外の例として、コインの表裏やupvote/downvote、クリックされたか否かのような2種類の事象を表せるベルヌーイ分布について考えてみましょう。たとえば、をいいねが押された確率とします。試行回数をNとしたとき、ベルヌーイ分布の和は二項分布
に従います。その期待値と分散はそれぞれ
、
であることから、平均分布の期待値と分散はそれぞれ
、
となります。そうすると、信頼区間は以下のように計算できます。
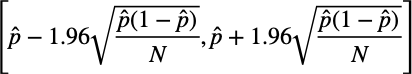
ベルヌーイ分布を正規近似することで、信頼区間の下限を求めることはできますが、ある状況下ではあまり良い近似をできません。そのような場合に使われるのが以下に示したWilson score intervalです。は何%信頼区間を使うかによって変わる値で、95%信頼区間なら
です。正規近似に比べると複雑な形をしていますが、簡単に導くことができます。導出についてはAppendixを参照してください。
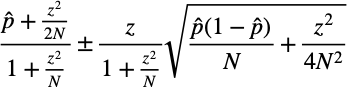
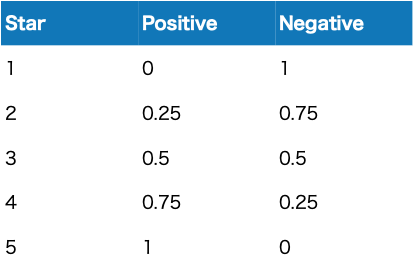
ここまでは二種類の値のみを扱ってきましたが、これを拡張することができます。たとえば、5段階評価の場合を考えてみましょう。そのような場合、星1ならupに1、downに0、星3ならupに0.5、downに0.5、星4ならupに0.75、downに0.25というように値を割り当てます。そうすると、その平均と分散を求めることができるので、Wilson score intervalを使うことができます。
スムージングの導入
平均評価による手法の問題点として、評価数が0の場合にスコアが不定になるという問題があります。どういうことかというと、平均評価については以下の式で求めることができますが、評価数が0の場合はとなり、平均を計算することができないということです。
この問題に対する一つの解としては、自然言語処理でよく使われているスムージング(smoothing)が挙げられます。スムージングとは何かと言うと、分母と分子に小さな数を割り当て、どんなものにも小さな確率を割り当てる処理のことです。たとえば、をすべての評価の平均、
をスムージングのパラメータとすると以下のように定義することができます。
式だけ見ててもわからないので、値を当てはめてみましょう。今、全体の評価の平均を、
とします。そうすると、評価数が0の場合にはスムージングした結果は3になります。つまり、評価が存在しない場合は全体の平均値を割り当てることができます。
また、この式では評価数が多いほどスムージング前の平均に近づくという性質があります。たとえば、評価4のデータが一つだけの場合は、スムージング結果は3.5になり、評価4のデータが10あれば結果は3.91、1000あれば3.99になります。
おわりに
今回は平均評価による推薦の問題点とその対策方法を紹介しました。平均評価による推薦に信頼区間の下限を使うことである種の確信度を考慮した推薦をできるようになるというメリットがあります。次回はベイズ的なアプローチについて紹介したいと思います。
Appendix
正規分布の再生性
正規分布の再生性というのは、確率変数と
が独立に正規分布
,
にそれぞれ従うとき、
+
も正規分布に従うというものです。また、その分布は
となります。
先の例の場合、N個の評価が平均
、分散
の正規分布
に従って独立に付けられると仮定しました。そうすると、その和の分布は正規分布の再生性により、
に従います。
ここから平均分布を求めるには、和の分布をNで割れば求めることができます。これには、期待値と分散に関する定数倍の公式を使うことができます。簡単なので以下にその証明を示しました。ここでの証明は離散分布に対する証明ですが、連続分布に対しても同様に証明することができます。
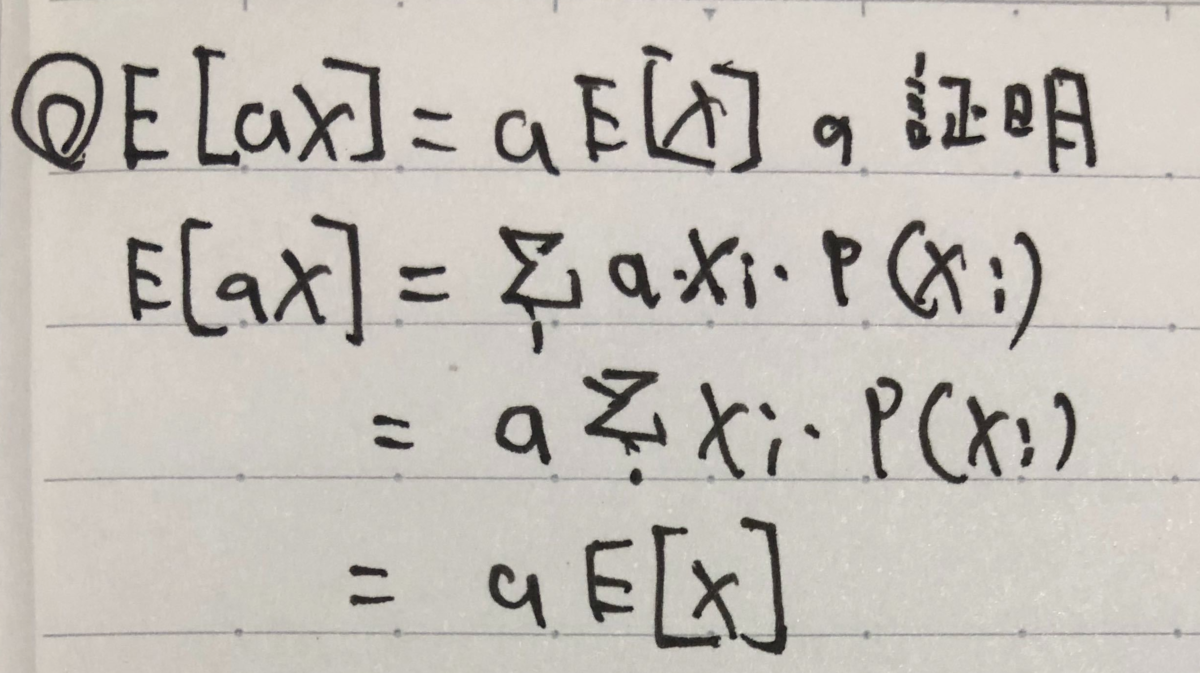
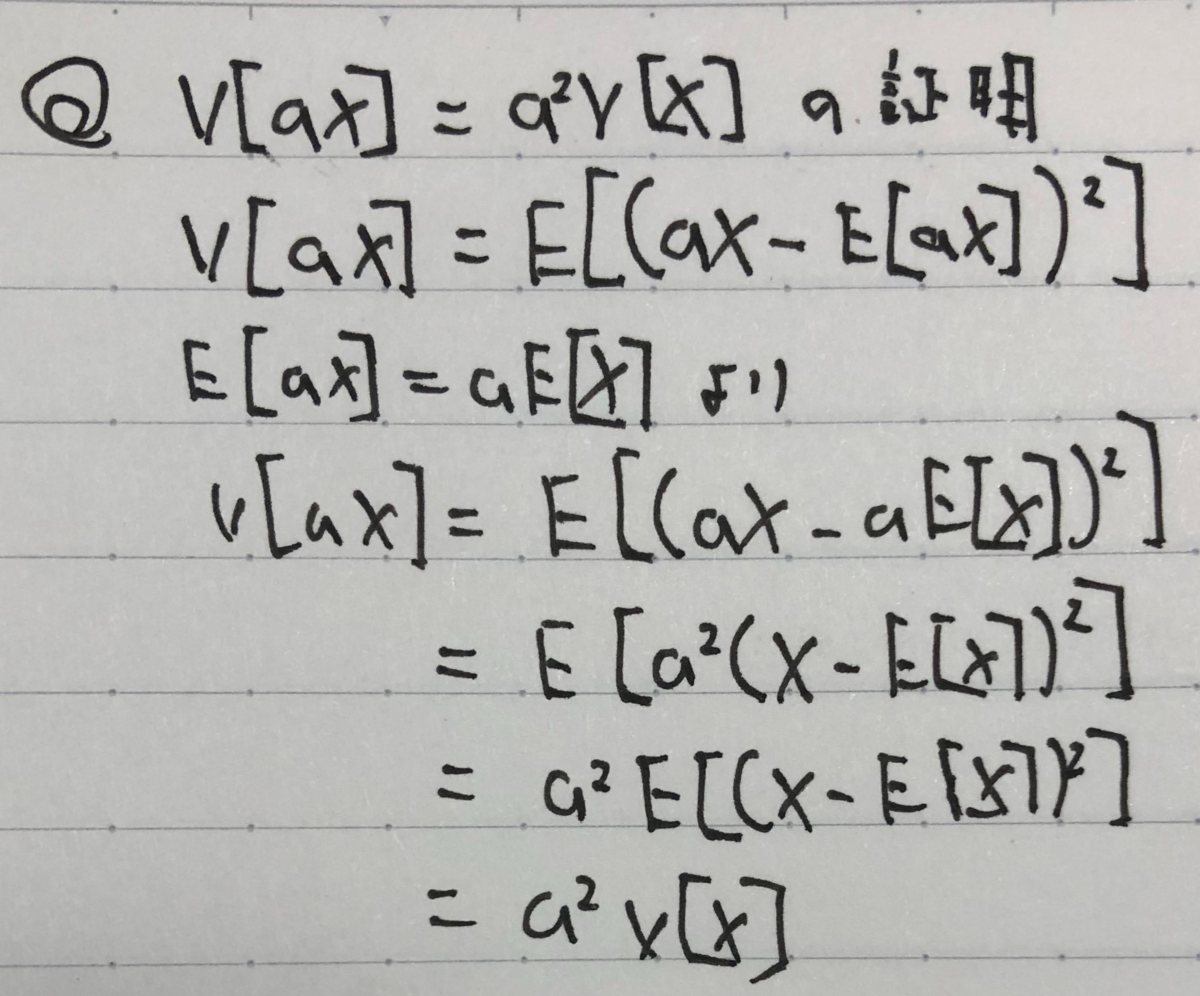
これらの式を使うことにより、平均分布はに従うことがわかります。したがって、評価数が増えれば分散が小さくなり、結果としてグラフが尖った形になるということです。
Wilson score intervalの導出
